光學顯微鏡發揮了核心作用，幫助理清復雜的生物學奧秘自從十七世紀荷蘭發明家安東尼凡列文虎克，英國科學家羅伯特·胡克首先報道分別使用單鏡頭及復合顯微鏡，觀察。在過去的三個世紀中，廣大的技術開發和制造的突破導致了顯著的*的顯微鏡設計，極大地提高了圖像質量，以*小的像差。然而，盡管計算機輔助光學設計和自動化磨削方法用來制造現代的鏡頭組件，基于玻璃顯微鏡仍然阻礙征收可見光的波陣面的衍射光學分辨率極限，因為他們通過圓形在物鏡的后焦平面的光圈。其結果是，可達到的*高點至點的分辨率，可以用光學顯微鏡得到的，是由一組基本的物理定律，可以很容易地克服由物鏡或光圈設計合理交替。這些分辨率的限制通常被稱為衍射障礙，這限制了光學儀器的能力區分的兩個對象之間的橫向距離小于大約一半的光的波長，用于圖像試樣分離。

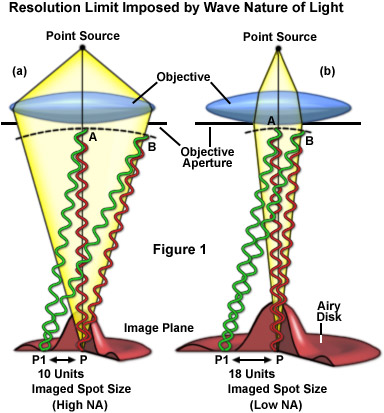
衍射的過程中涉及的光波的傳播時，與構成一個典型試樣的錯綜復雜的結構。由于這樣的事實，在顯微鏡中觀察到的大多數試樣組成的高度重疊的功能，*好是表示的多個點光源，討論的描述代表一個單一的點光源的光通過波陣面通過顯微鏡衍射阻擋中心各種光學元件和光圈隔膜。正如下面將要討論的那樣，透射光或熒光發射波陣面所產生的衍射物鏡孔徑的邊緣顯微鏡檢體平面中的一個點，有效地傳播的波陣面，以產生圖像，綻開的點源有限的磁盤具有一個中央的衍射圖案，但較大的尺寸比原來的點。因此，由于光的衍射，檢體的圖像永遠不會**地表示存在于試樣中的真實的細節，因為有一個下限，低于顯微鏡的光學系統的結構細節不能解析。

除了發散光波在光學儀器中所發生的衍射現象，干擾的過程中描述的重組和求和的兩個或更多個重疊的波陣面。光的干涉也許是*普遍的現象，在光學顯微鏡和圖像形成的各個方面發揮著核心作用。在熒光或激光掃描共聚焦顯微鏡，物鏡的作用是集中到一個焦點的激發光的聚焦在試樣平面上的波前，以確保相長干涉。在此要求，建設性的干擾（下面討論），確保從所有可用的物鏡孔徑角入射的波陣面的電場矢量駐留在相同的相位，因此產生*小的可能的激勵點。

這兩個干涉和衍射，這實際上是表現為相同的過程，是負責創建在中間像平面在顯微鏡試樣的實像。簡單地說，兩個波陣面之間的干擾的發生，此外，如果波是**的相（建設性的干擾）的振幅的兩倍，但波互相抵消時完全出了180度的相位（稱為破壞性干擾，但大多數發生干擾介于兩者之間）。光子的能量光波固有本身不是一倍，或全軍覆沒兩波干擾時，而這種能量在允許建設性的干擾方向的衍射和干涉。因此應被視為涉及光波和光子能量的再分配現象，干涉和衍射。

A點對象中的顯微鏡，如熒光的蛋白質單分子，產生圖像干擾的作用產生的衍射圖案由上面的中間平面。當高度放大的，觀察到的點對象的衍射圖案包括一系列的衍射環所包圍的一個中心位置（衍射磁盤）（參見圖1）。在與衍射理論的命名法中，明亮的中心區域被稱為環的零級衍射點，而被稱為*，第二，第三，等等，為了衍射環。當顯微鏡是正確的集中，在極小環之間的光的強度是零。相結合，這點光源的衍射圖樣被稱為的艾里磁盤（喬治爵士后B.艾里，十九世紀英國天文學家）。的大小的艾里圖案的中心的位置，相關的光的波長和物鏡的孔徑角。顯微鏡的物鏡，孔徑角所描述的數值孔徑（NA），其中包括了長期的罪θ，*過該物鏡可以收集來自試樣的光的角的一半。在分辨率方面，在橫向衍射艾里斑的半徑（Y）圖像平面是由下式定義：

阿貝分辨率_X，：Y =λ/2NA （1）。

其中，λ是照明的透射光或熒光的激發波長頻帶的平均波長。的物鏡的數值孔徑（NA =sin（θ））由成像介質的折射率（N，通常是空氣，水，甘油，或油）的孔徑角的正弦值乘以（sin（θ）被定義）。其結果是在此關系中，由一個點光源產生的光斑的大小隨波長和增大數值孔徑減小，但始終保持有限直徑的磁盤。因此，圖像產生的具有綠光（550納米）的數值孔徑為0.90的100倍放大倍率的物鏡的光點尺寸是約30微米，而通過100x物鏡的數值孔徑1.4的光點尺寸是約200納米，近50 ％較小。衍射極限分辨率的理論在1873年由德國物理學家恩斯特·阿貝墊付（見公式（1） ），后來提煉瑞利勛爵在1896年（ 方程（3） ），以必要的兩個艾里圖案之間分離，以定量措施區分它們作為獨立的實體。

阿貝分辨率_? =2λ/NA ² （2）

根據阿貝的理論，圖象是由具有不同強度的衍射限制的點重疊，以生成*終的結果，如上所述的從數組中。因此，優化的空間分辨率和圖像的對比度的*機制是通過減少成像波長，增大數值孔徑，或使用具有較大的折射率的成像介質的衍射限制的點的大小*小化。然而，在理想條件下具有***的物鏡，橫向分辨率仍然有限相對溫和的水平，由于傳輸特性的影響玻璃接近200至250毫微米（見公式（1） ），在波長400納米下的數值孔徑的物理約束。與此相反，在艾里斑的軸向尺寸，通常被稱為的點擴散函數（PSF）形成一個橢圓形的圖案。沿著光軸的點擴散函數的幾何形狀的細長來自非對稱的波陣面，從顯微鏡物鏡的性質。在光學顯微鏡軸向分辨率甚至不如橫向分辨率（公式（2）中所概述），500納米的順序。當試圖高度曲折的圖像的功能，如細 胞器，衍射限制的分辨率表現為不良軸向切片能力，并降低對比度在成像平面上。此外，整體實現三維標本的標本的對比焦點外的光的干涉的點擴散函數的發生是由于相對較差的軸向分辨率一般是占主導地位的。

圖1中所示的衍射斑的大小在一個典型的光學顯微鏡物鏡孔徑角的效果。示出的點源和它的共軛（P）在圖像平面的波陣面會聚，并進行建設性干涉的物鏡具有較大（圖1（a）段）和小（圖1（b））的數值孔徑。的點P1在焦平面上橫向移動，直到在一定的距離的相消干涉（取決于物鏡的數值孔徑）定義的位置的的*衍射*低的，因此衍射點的半徑。對于高分辨率的配置在圖1（a），分甲和乙的波陣面產生10任意單位定義成像光斑尺寸更小的光斑尺寸。與此相反，在圖1（b）的較低分辨率的配置，降低孔徑角增加甲和乙至18任意單元之間的距離。換言之，由熒光團發射的光（點光源）移動同樣的距離的波陣面到達在影象平面上的相位和干涉產生具有高強度的光點在圖像平面上的物鏡聚焦。相消干涉，從而導致強度為零，所產生的波陣面到達分之一波長的相位（見上面的討論）。由于強度下降是逐漸現貨沿著橫向軸線，將出現兩個點源（或熒光分子）緊密聯系起來的光斑的大小是一個單一的，較大的光斑和未解決的。

如上所述，在三維空間中的艾里斑的光強分布是指作為一個點擴散函數和完整地描述了一個點光源的光的衍射圖案的（例如作為一個單一的熒光基團）在橫向 ( x , y ) 修改受衍射限制的光學顯微鏡的軸向（z）的尺寸。點擴散函數的大小來確定成像光的波長的特性的物鏡（數值孔徑）和成像介質的折射率。分辨率，在實際意義上，通常被定義為*小之間的間隔距離的兩個點狀的物體中，仍可以將它們作為單獨的發射器（未合并成一個單一的點）區別。其結果是，大多數的分辨率標準（例如，瑞利判據，麻雀限制，或*大值一半處的全寬度，半峰全寬）直接相關的點擴散函數的性質和幾何形狀。

Rayleigh分辨率_X，：Y =0.61λ/NA （3）

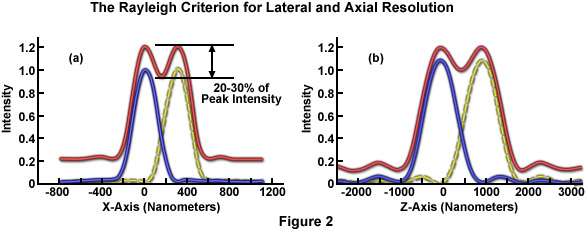
根據瑞利判據，在顯微鏡中觀察到的兩個點源被視為被解決時的艾里斑的光點中心的主要衍射峰（見圖2）從一個點源與**小重疊（暗區域圍繞中央的艾里斑）等點源。如果兩個艾里磁盤或點擴散函數之間的距離大于該值，這兩個點源被認為是要解決（和可以很容易地加以區別）。否則，艾里磁盤合并在一起，被認為是不被解決。其他條款中所述，瑞利判據被滿足的時候，兩個緊密間隔的點源的圖像之間的距離的點擴散函數的寬度是約等于。相比之下，兩個點源的圖像不再有浸在中央峰之間的亮度，而是表現出恒定的亮度，跨區域之間的峰之間的距離被定義為Sparrow分辨率極限。Sparrow分辨率極限是阿貝值的大約三分之二（公式（4） ）的瑞利分辨極限。

Sparrow分辨率_X，：Y =0.47λ/NA （4）

圖2給出了瑞利判據的兩個緊密定位的點聲源的側向和軸向尺寸的圖形表示。在圖2（a）中，點源的強度表示固體藍色，黃色虛線的曲線。的合并點源產生的位移沿縱坐標為清楚起見，一個紅色的曲線表示的總強度。為了區分這些點源，峰之間的距離應足以產生，取值范圍在20和30％的強度的峰值（圖2（a））的強度*小。同樣的標準適用于的軸向尺寸（圖2（b））。請注意，分辨率（在圖2（a）和圖2（b）沿橫坐標表示）是沿z軸的顯著較低的。

雖然瑞利判據和類似措施是有效分辨率壓力表觀察的標本，仍然有幾個缺點，這樣的定義分辨率。例如，在研究者注意，兩個粒子合并，以形成一個單一的點圖像的情況下，計算機算法可以適用于區分的粒子以任意小的距離。確定兩個相鄰的粒子的精確位置，然后就變成了實驗精度的問題，而不是所描述的瑞利限制決定的光子統計。此外，分辨率的限制并不一定對應的細節，可以在圖像中觀察到的水平。雖然瑞利極限的距離被定義為從**小值的點擴散函數的中心，這個值可以被呈現的*的光學系統或線性光學小。分辨率標準，也不要依賴于燈是一種衍射波陣面構成一定的限制的詳細程度，實際上是包含在浪的事實。

分辨率阿貝方程避免瑞利判據和麻雀限制的缺點，但有一個更間接的解釋。可成像的過程中，在顯微鏡中的樣本之間的照明和熒光發射（或透射光）的點擴散函數的卷積運算。被進行傅立葉變換（參見圖3）后，在顯微鏡觀察對象（無論它們是周期性的或不）都可以被*地描述為眾多具有不同空間頻率的正弦曲線的總和。需要注意的是檢體的圖像，存在于所有的共軛像平面，存在的傅里葉變換在更高的頻率代表細標本細節和較低的頻率代表粗細節（圖3（a））中的相應的孔的平面。這點與物鏡后孔中的波形，圖3（b）中示出。較低的空間頻率位于光圈的中心附近，而頻率接近的孔的邊緣的區域逐漸增大。

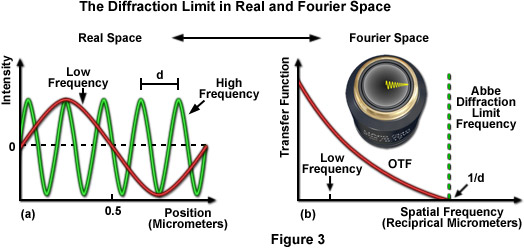
在實際空間中的卷積的概念可以容易地通過檢查在傅立葉空間中的等效操作簡化。在后者中，可以乘以變換的對象，得到沒有噪聲的理想圖像的傅立葉變換的點擴散函數的傅里葉變換。點擴散函數的傅立葉變換后，描述了每個試樣的空間頻率如何有效地被轉移到*終的圖像。因此，在傅立葉變換后的點擴散函數是指作為光學傳遞函數（OTF，請參閱圖3（b））。OTF定義在何種程度上含有標本信息丟失的空間頻率，保留，減毒，或在成像過程中的相移。在成像過程中丟失的空間頻率信息，無法恢復，所以各種形式的顯微鏡的主要物鏡之一是盡可能獲得*高的頻率范圍為標本。在每個空間頻率的OTF（測量在振蕩每米）的值是一個有用的指標，來描述一個特定的正弦對象特征的對比度達到在*終圖像中。

要記住的光學顯微鏡的重要口岸之一是檢測光學傳遞函數的特征頻率，作為一項決議，“截止”邊框（阿貝極限頻率;參見圖3（b））。在圖像中不存在記錄，可通過在顯微鏡高于限值的頻率。的*高空間頻率的峰到峰的距離，因此，能夠通過的物鏡（在圖3中的波形為綠色（一））的值e阿貝限制，這是更正式的定義為通常被稱為在一個結構中，可以在*終圖像中檢測到的*小的周期。由于這樣的事實，一個點光源發出或傳送的空間頻率范圍廣泛，阿貝限制也必須跨越三個維度中的點擴散函數。

結論

傳統的廣角鏡產生圖像捕捉光線在不同的地點在物鏡上進一步加工的波陣面為通，通過光的火車，終于干擾在圖像平面的點源。其結果是在光學的互易原理，阿貝限制在顯微鏡的橫向軸線的兩波干擾的物鏡捕獲在*極端的角度，可以通過以下方式獲得的*大的*大距離相對應。的阿貝分辨率極限是有吸引力的，因為它僅依賴于離開試樣的物鏡捕獲的不同的波陣面之間的*大相對角度。此限制，因此介紹的*小級別的細節，都不可能進行成像，并周期性結構具有較高的空間頻率（波長較短）將不會傳送到圖像。

即使在用光學顯微鏡配有可用的*高質量的透鏡元件，是完全一致的，并具有*高的數值孔徑的情況下，分辨率仍僅限于大約一半的光的波長在*好的情況下。在實踐中，通常實現在常規成像的分辨率往往達不到衍射的物理限制。這是由于這樣的事實，在試樣的光學不均勻性可以激發光束的相位失真，導致一個重點的體積明顯大于衍射限制的想法。此外，分辨率也可以通過使用不兼容的浸油損害，蓋玻片具有的*佳范圍以外的厚度，調整不當校正鋌。

已被廣泛使用激光掃描共聚焦和多光子顯微鏡適度提高沿橫向和軸向的軸的空間分辨率，但這些技術仍然有限的方面實現顯著改善。加上針孔限制在共聚焦顯微鏡檢測的聚焦激光激發，在原則上，由1.4倍提高空間分辨率，雖然這只有在信號與噪聲在一個顯著的成本實現。同樣地，多光子熒光顯微鏡利用非線性吸收過程，以減少有效的激發點擴散函數的大小。但是，再次，更小和更精細的點擴散函數被抵消的必要性，使用較長波長的激勵光。作為一個結果，而不是提供顯著改善的分辨率，共聚焦和多光子顯微鏡比傳統的廣角技術的主要優點是減少排放源的焦平面（焦亮），使去除背景信號源自三維容積重建成像方式獲得清晰的光學部分。

由物理定律支配光學顯微鏡的分辨率限制，可以*過，但是，通過利用法律的“漏洞”，強調的事實是真實的，只有在一定的假設下的局限性。存在特別重要的三個假設分辨率標準的評估過程中發揮作用，包括常規的幾何形狀，其中所收集的物鏡，整個試樣的激勵光的均勻性，線性特性（吸收和發射）的熒光光涉及單個光子。簡單地說，通過收集周圍的試樣或使用隨位置而變化的激勵光的光在一個較大的角度，可以提高分辨率。使用熒光的過程，涉及兩個或兩個以上的光子在一個非線性的方式，也可以分解的衍射屏障。