在顯微術中，術語“分辨率”用于描述顯微鏡區分細節的能力。換句話說，這是通過觀察者或顯微鏡攝像機仍然可以看到樣本的兩個不同點的*小距離 - 作為單獨的實體。

顯微鏡的分辨率與光學部件的數值孔徑（NA）以及用于檢查樣品的光的波長本質上相關。此外，我們必須考慮由恩斯特·阿貝（Ernst Abbe）于1873年首次描述的衍射極限。

本文涵蓋了這些概念背后的一些歷史，并解釋每個使用相對簡單的術語。

分辨率和數值孔徑

數值孔徑（NA）與光通過的介質的折射率（n）以及給定物鏡（NA = n x sinα）的角孔徑（α）有關。顯微鏡的分辨率不僅僅取決于物鏡的NA，而是考慮到顯微鏡聚光鏡的NA，整個系統的NA。更多的圖像細節將在其中所有光學部件正確對準，具有相對較高的NA值并且彼此協調工作的顯微鏡系統中被解決。分辨率也與用于對樣本成像的光的波長有關; 較短波長的光能夠比較長的波長分辨更多的細節。

在處理決議時需要考慮三個數學概念：“阿貝衍射極限”，“艾里光盤”和“瑞利標準”。這些都按時間順序列在下面。

喬治·比德爾·艾利和“艾利斑”（1835）

喬治·比德爾·艾利（George Biddell Airy 1801-1892）是英國數學家和天文學家。到1826年（25歲），他被任命為三一學院數學教授，兩年后，他被任命為新劍橋天文臺的天文教授。從1835年到1881年，他是“天文學家皇家”，他有一個月球和火星火山口以他的榮譽命名。

同樣在1835年，他在劍橋哲學社會交易會上發表了一篇題為“關于圓形玻璃的衍射”的論文。艾里從天文學家的角度非常地寫了這篇文章，他描述了“在一個好的望遠鏡上看到的星星的形象和光線的形狀和亮度”。盡管在不同的科學領域寫作，但這些觀察結果與其他光學系統和顯微鏡相關

的艾里斑是可以通過一個圓形孔在通過衍射限制的完全對準的系統來確定的光的*佳聚焦點。從上圖（圖1）可以看出，這是一個亮點，它們是同心環或波紋（更準確地稱為通氣圖案）。

衍射圖案由光的波長和光通過的孔的大小確定。Airy Disc的中心點包含大約84％的發光強度，其余16％在衍射圖案周圍。當然，用顯微鏡觀察到的樣本中有許多光線，而且像“Airy Disc”一詞所描述的那樣，更適合多種艾里模式而不是單點光。

如圖1下半部分所示的艾里模式的三維表示也稱為“點擴展函數”。

恩斯特·阿貝和“阿貝的衍射極限”（1873）

恩斯特·卡爾·阿貝（Ernst·Karl·Abbe 1840-1905年）是德國數學家和物理學家，1866年，他遇到卡爾·蔡司，并共同創立了所謂的“蔡司光學工程”，現在被稱為蔡司。此外，他還于1884年共同創立了Schott Glassworks。阿貝也是*個定義術語數值孔徑的人。1873年，阿貝出版了他的理論和公式，解釋了顯微鏡的衍射極限。阿貝認識到標本圖像由多個重疊的多重強度的衍射極限點（或艾里版）組成。

為了提高分辨率（d =λ/ 2 NA），必須使用較短波長（λ）光或通過具有較高折射率的成像介質或具有高NA的光學部件（或，實際上是所有這些因素的組合）。

然而，即使考慮到所有這些因素，由于整個系統的復雜性，波長在400nm以下的玻璃的傳輸特性以及在完整的波長下達到高的NA，實際顯微鏡系統的限制仍然有限制顯微鏡。理想光學顯微鏡中的橫向分辨率限制在約200nm，而軸向分辨率約為500nm（例如分辨率限制，請參見下文）。

約翰·威廉·斯特拉特和“瑞利標準”（1896）

約翰·威廉·斯特魯特（John William Strutt），3rd Baron Rayleigh（1842-1919）是英國物理學家和多產作家。他在一生中寫了***的466篇出版物，其中包括430篇科學論文。他寫了一系列廣泛的主題，如鳥飛，心理研究，聲學等，并于1895年發現了氬氣（他于1904年被授予諾貝爾物理學獎）。

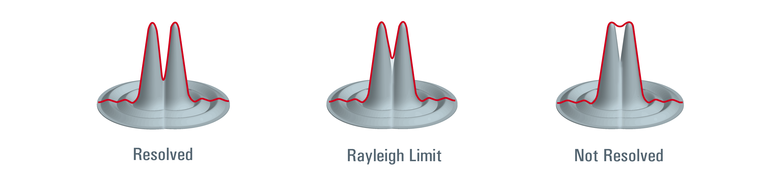
瑞利建立并擴大了喬治·艾里的作品，并于1896年發明了“瑞利標準”的理論。瑞利標準（圖2）定義了衍射受限系統中的分辨率極限，換句話說，當兩點光可以區分或相互分離。

使用艾里光盤的理論，如果來自兩個單獨的艾里版光盤的衍射圖案不重疊，則它們很容易區分，“很好地解決”，據說符合瑞利標準（圖2，左圖）。當一張艾里光盤的中心直接與另一張**的衍射圖案的*個*小值重疊時，它們可以被認為是“剛剛解決”，并且仍然可以區分為兩個獨立的光點（圖2，中間）。如果艾里光盤比這更接近，那么它們不符合瑞利標準，并且“未被解析”為兩個不同的光點（或標本圖像中的單獨細節;圖2右側）。

圖2：由兩個單獨的艾菲片重疊衍射圖所示的分辨率極限（由瑞利標準定義）：
左：解決中：剛解決右：未解決

如何計算顯微鏡的分辨率

考慮到上述所有理論，很明顯，在計算理論分辨率極限時，需要考慮許多因素。分辨率也取決于樣本的性質。我們來看看使用阿貝的衍射極限計算分辨率，并使用瑞利標準。

首先，應該記住：

NA = n x sin α

其中n是成像介質的折射率，α是物鏡的角孔的一半。物鏡的*大角度孔徑約為144o。該角度的一半的正弦為0.95。如果使用折射率為1.52的油的浸沒物鏡，物鏡的*大NA將為1.45。如果使用“干式”（非浸沒）物鏡，物鏡的*大NA將為0.95（空氣的折射率為1.0）。

橫向（即XY）分辨率的阿貝衍射公式為：

d =λ/ 2 NA

其中λ是用于成像樣品的光的波長。如果使用514nm的綠光和NA為1.45的油浸物鏡，則分辨率的（理論）極限將為177nm。

軸向（即Z）分辨率的阿貝衍射公式為：

d = 2λ/ NA²

再次，如果我們假設波長為514nm，以NA值為1.45的物鏡觀察樣品，則軸向分辨率將為488nm。

瑞利標準是基于阿貝的衍射極限的一個略微改進的公式：

R =1.22λ/ NAobj + NAcond

其中λ是用于成像樣品的光的波長。NAobj是物鏡的NA。NAcond是聚光鏡的NA。“1.22”的數字是一個常數。這是從瑞利關于貝塞爾功能的工作得出的。這些用于計算諸如波傳播的系統中的問題。

考慮到聚光鏡的NA，空氣（折射率為1.0）通常是聚光鏡和載玻片之間的成像介質。假設聚光鏡的角度孔徑為144°，則NAcond值將等于0.95。

如果使用514nm的綠光，NA為1.45的油浸物鏡，NA為0.95的聚光鏡，則（理論）分辨率極限為261nm。

如上所述，用于對樣本進行成像的光的波長越短，則將更多的細節被解決。因此，如果使用400nm光的*短可見波長，使用NA為1.45的油浸物鏡和NA為0.95的聚光鏡，則R將等于203nm。

為了在顯微鏡系統中實現*大（理論）分辨率，每個光學部件應該具有*高的NA可用（考慮角度孔徑）。此外，使用較短波長的光來觀察樣品會增加分辨率。*后，整個顯微鏡系統應該正確對齊。