術語“ 透鏡”是通用名稱，考慮到玻璃或透明塑料材料的一個組成部分，通常是圓形的，直徑，有兩個主要的表面研磨和拋光，以特定的方式，以產生一個光通過會聚或發散的的材料。 在光學顯微鏡形成的標本放在載物臺上，通過來自所述照射器的光通過一系列的玻璃透鏡，該光聚焦到目鏡中的任何一個，在一個傳統的照相機系統的膜平面的圖像，或一個的表面上數字圖像傳感器。

受折射和反射的原理，在顯微鏡中使用的許多的類似，一個簡單的透鏡的作用下借助涉及追蹤光線通過透鏡的幾何形狀的一些簡單的規則可以被理解。 在這次討論中探討的基本概念，這都源于科學的幾何光學 ，會導致理解的放大過程，實像和虛像的屬性，以及鏡頭畸變或缺陷。

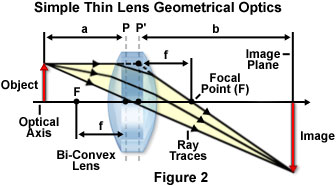
為了理解一個簡單的顯微鏡的光學系統（在圖1中的奧林巴斯顯微鏡，在一個共同的實驗室顯微鏡的透鏡元件的位置），一個簡單的薄透鏡，其具有兩個光折射的表面和中心光軸的基本屬性，必須先進行說明。 每個透鏡有兩個主平面和兩個焦平面的幾何形狀的透鏡和透鏡和聚焦圖像之間的關系所定義的。 通過透鏡的光線相交的物理團結的焦平面上（參見圖2），進入鏡頭的光線相交于新出現的光線從透鏡的主平面與擴展而擴展。 的焦距的透鏡的主平面和焦平面之間的距離被定義為，每個透鏡都具有一組這些平面的每一側（前和后）。

通過一個簡單的雙凸透鏡薄板玻璃透鏡的光線的軌跡是在圖2中，一起形成聚焦圖像的射線所必需的其他重要幾何參數。 由變量 F表示透鏡的焦點，有兩個單獨的聯絡點，一個在前面的透鏡（在 圖2中的左手側）和一個后面的透鏡（在 右邊）。 透鏡的主平面（P和P'在圖2中），用虛線表示，而每個主平面之間的距離和其各自的焦點代表的焦距（f）。 由于圖2中所示的雙凸透鏡是對稱的，位于主平面的透鏡表面的距離相等，前部和后部的焦距也相等。

由透鏡成像的對象（或樣品）中的物體面位置，位于左手側的鏡頭，按照慣例，并行進向上的中心線或光軸，它傳遞一個紅色箭頭表示的通過透鏡的中心，垂直于主平面。 通過透鏡的光線追跡（黃色箭頭）源自的對象，并通過透鏡形成的放大的實像（反轉紅色箭頭）在圖像平面上的右手側的透鏡，進行由左到右。 前側主平面的透鏡和被檢體之間的距離被稱為對象的距離 ，由變量 a在圖2中表示。 從后方的主平面的距離的圖像（在圖2中的變量b）以類似的方式，被稱為圖像進行距離 。 這些參數是定義一個簡單的透鏡的幾何光學的基本元素，并可以用來計算重要的屬性，包括焦距和倍率的鏡頭。

透鏡可以是正的或負的 ，這取決于它們是否會造成光線通過收斂成一個單一的聯絡點，或從光軸向外發散到空間。 在圖2和圖3中示出）的正透鏡（會聚平行于光軸入射的光線集中的焦平面上形成的實像。 正透鏡如圖3所示，有一個或兩個凸表面，并在中心比邊緣厚。 的正透鏡中的一個共同特點是，它們時，它們被放置物體和人眼之間的物體放大。 與此相反，負透鏡發散平行的入射光線的光線通過透鏡到焦點鏡片后面的痕跡延伸形成的虛像。 負透鏡具有至少一個凹面和較薄的中心比邊緣（參見圖3）。 當負透鏡之間放置一個對象，并在眼睛，并沒有形成一個真正的圖像，但會降低（或demagnifies）所形成的虛像的對象的外觀尺寸。

一個真正的虛像之間的區別是一個重要的概念，當通過透鏡或反射鏡系統的成像標本時，不管系統是否由單個或多個組件。 在一般情況下，被定義為圖像的光線（和它們的擴展）的區域成為會聚折射的結果，通過透鏡或反射鏡由。 在光線相交的情況下，在焦點中，圖像是真實的，可以在屏幕上觀看，錄制在膠片上，或投射到諸如CCD或CMOS傳感器的表面的圖像平面中的下。 當光線發散，但項目虛擴展，匯聚到一個焦點，形象是虛擬的，不能在屏幕上觀看或錄制在膠片上。 為了進行可視化，必須形成一個真正的圖像上的眼睛的視網膜。 通過目鏡的顯微鏡觀察時，在視網膜上形成的實像，但它實際上是觀察者所感受到的存在，作為一個虛擬的距離約為10英寸（25厘米），在前面的眼睛的圖像。

主透鏡的幾何形狀，圖3中所示的正透鏡元件是雙凸透鏡 （圖3（a））， 平凸透鏡 （圖3（b）具有一個平面或平坦的表面）。 此外， 凸彎月面 （圖3（c））的透鏡同時具有相似的曲率的凸面和凹面，但在中心比邊緣厚。 雙凸鏡片是最簡單的放大鏡，并有一個聯絡點，取決于表面的曲率角倍率。 更高的角的曲率導致較短的焦距，由于這樣的事實，在更大的角度相對于光軸的鏡頭折射光波。 雙凸鏡片的對稱性質，最小化的圖像和對象的應用中，對稱地位于球面像差。 當雙凸透鏡的光學系統是完全對稱的（實際上，以1:1的放大倍率），球面象差是一個最低值和彗差和畸變同樣最小化或取消。 一般來說，雙凸透鏡執行以最小的畸變，在放大倍率0.2倍和5倍之間。 凸透鏡主要受聘為重點的應用程序和圖像的放大倍率。

典型的平凸透鏡（圖3（b）條）有一個正的相對側上的透鏡的凸面和一個平面（平）面。 這些鏡片平行光線集中到一個焦點，是積極的，形成了一個真正的圖像可以投射或操縱空間濾波器。 不對稱的平凸透鏡的球面像差最小化的應用程序中的對象和圖像在于從透鏡的距離不等。 理想的情況下，以減少像差的發生，當對象被放置在無窮遠（實際上，平行光線進入鏡頭）和圖像是最后的聚焦點。 然而，平凸透鏡會產生最小像差以共軛的比例大約為5:1。 當向著物體的平凸透鏡的彎曲表面的方向，調焦盡可能精確的實現。 平凸透鏡是有用的發散光束準直，并且將焦點放到一個更復雜的光學系統。

正彎月形透鏡（圖3（c））具有非對稱結構的一個表面形狀為凸半徑，而相反的面略凹的。 彎月形透鏡通常采用與另一個透鏡結合，以產生具有一個較長或較短的焦距比原來的透鏡的光學系統。 作為一個例子，正彎月形透鏡可被定位后，平凸透鏡的焦距縮短，而不降低光學系統的性能。 正彎月形透鏡的透鏡的凹面側上有較大的曲率半徑比凸側，使形成的實像。

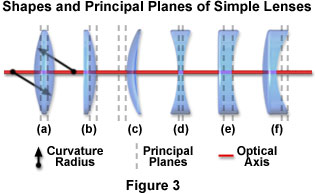
負透鏡元件（圖第3（d））的雙凹透鏡 ， 平凹透鏡 （圖3（e），與一個單一的平面表面）， 凹彎月面（圖3（f）），其中也有凹部和凸面，但比邊緣薄的透鏡的中心。 正面和負面的彎月形透鏡的表面和其焦平面之間的距離是不相等的，但其焦距是相等的。 的透鏡曲面的中心連接起來的線，在圖3中被稱為透鏡的光軸。 具有對稱的形狀（雙凸或雙凹透鏡）的簡單的透鏡的主平面，在圖3中，用虛線表示相對于彼此和透鏡面是等間距的。 為雙凸透鏡的凸面的曲率半徑在圖3（a）中由黑色箭頭表示。 彎月形透鏡和在平的負和正透鏡，其他的透鏡，如對稱的缺乏導致的主平面的位置，根據透鏡的幾何形狀而有所不同。 平凸透鏡，平凹透鏡有一個主平面的光軸相交，在邊緣的彎曲表面，埋在里面的玻璃和其他平面。 彎月透鏡的主平面之外的鏡頭表面。

雙凹透鏡（圖第3（d）），主要用于發散光束和圖象尺寸的減少，以及增加光學系統的焦距，會聚光束的準直。 通常被稱為雙凹的透鏡，該光學元件折射并行輸入射線發散，使他們相差的光軸在透鏡的輸出側上，在前面的鏡頭形成負的焦點。 雖然輸出光線實際上不聯合起來，形成一個焦點，但會出現發散的虛像位于物體側的透鏡。 雙凹透鏡可以耦合到其他的透鏡，以減少光學系統的焦距。

圖3（e）中所示的平凹透鏡發散元件，具有負的聯絡點，并產生一個虛擬的圖像。 當準直光束入射的平凹透鏡部件的彎曲表面上，出射側形成的發散光束。 該光束將出現出現從一個較小的虛擬點聲源的比，如果平面的透鏡表面所面臨的準直光束。 平凹鏡頭時具有最小的球面像差凹面面臨的共軛距離最長，擴大光束或增加現有的光學系統的焦距。

也稱為作為凹凸透鏡，負（發散）的凹凸透鏡可以被設計，以減少或消除，耦合透鏡光學系統中的額外的球面像差或彗差。 彎月形透鏡（正和負）通常采用縮短的雙重峰（膠合在一起的兩個透鏡元件）的焦距或平凸透鏡操作，在無限遠共軛比（平行光線照射）。 所需的最終系統的焦距決定的特定的尺寸和字符應該被添加的彎月形透鏡。 的Plano-convex/meniscus鏡頭組合顯示多達4倍分辨率比平凸透鏡單獨工作。

透鏡折射入射光波前點，在那里他們進入和退出的鏡頭表面。 折射的角度，因此，焦距，將取決于在透鏡表面的幾何形狀，以及所使用的材料來構造透鏡。 具有高折射率的材料，具有更短的焦距比具有較低的折射率的。 例如，合成的聚合物，如透明合成樹脂（折射率為1.47）制成的透鏡，有一個較低的比玻璃的折射率（1.51），導致稍長焦距。 璐彩特和玻璃的折射率幸運的是，如此接近，可以用有機玻璃取代玻璃在許多鏡頭應用，其中包括廣受歡迎的電影的一箱相機目前享有廣泛的消費者使用。 純凈的鉆石（2.42折射率）鏡片，焦距明顯低于玻璃或有機玻璃，雖然成本高純凈的鉆石將鏡頭建設望而卻步。

正如上面所提到的，所有的透鏡具有與透鏡的前表面和后表面的兩個主平面。 在顯微鏡，透鏡往往是膠合在一起以形成較大的組（ 厚透鏡）具有相當不尋常的主平面相對于透鏡面的位置。 然而，不管透鏡元件的數量或透鏡系統的復雜性，厚透鏡的主平面的位置可以由追蹤光線通過透鏡的準確的附圖。 現代的鏡頭設計師和光學工程師要用先進的計算機模型，設計方案，并跟蹤通過個別鏡頭的光線和多元素鏡頭系統。 這些軟件程序用于設計照相機，望遠鏡，顯微鏡，及其他光學元件，依靠玻璃（或塑料）透鏡，以形成圖像。

一般有三種規則適用于追蹤光線通過一個簡單的鏡頭（見圖2），這使得任務相對簡單。 首先，光線通過透鏡的中心從對象上的點繪制的圖像上的對應點（圖2中的箭頭的**）。 沒有偏離由透鏡，此射線。 其次，從最高點的對象發出的光線平行于光軸的方向繪制的，由透鏡折射后，將交叉并通過后焦點。 事實上，所有的平行于光軸的光線通過由透鏡折射后的后焦點。 第三，從物體的射線通過前焦點折射透鏡在平行于光軸的方向上具有相同的點，在圖像上重合。 剛才所描述的，通常被稱為特征射線 ，射線中的任何兩個的交叉點定義的鏡頭的像面。

個別光線追跡的概念擴展到光束是必要的描述光學顯微鏡中發生的事件。 當平行光束的光通過一個簡單的透鏡的光線被折射，并濃縮成一個聚焦光點的光的鏡頭的焦點處（在圖2中的點 F）。 另外，位于鏡頭的焦點從一個點源的光進入鏡頭時，它的出現為近軸平行光束。 從顯微鏡照明源的光可以被視為一列光波，彼此同相振動。 波列與此相關聯的波前是在一個平面上的垂直于傳播方向（通常是平行于光軸的顯微鏡），并轉換成一個球面波時，通過一個簡單的雙凸透鏡。 鏡頭的焦點，集中在半徑的球面波和光波到達相，并進行建設性的相互干擾（添加劑）的焦點。 是一個點光源的情況下，從一個簡單的透鏡的焦點發出的球面波前轉換成平面波前時所發生的通過透鏡通過折射。

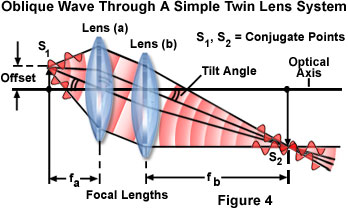
甲穿越空間的平面波前往往是不垂直于光軸的透鏡，而是一些從軸線傾斜時的入射角到達。 中心的球面波通過透鏡的離軸平面波通過的結果在某些點相差的透鏡的光軸位于。 出于實用的目的，可以被認為是平面波半徑無限大的球面波，它可以通過透鏡聚焦到另一個具有一個更小的半徑等于焦距的鏡頭的球面波。 因此，可以得出結論，一個簡單的雙凸透鏡的工作由一個球面波轉換到另一個球面波，經常與不同的半徑（或聯絡點）。 此外，第二球面波的曲率中心位于在透鏡的焦平面上。

如果不在于透鏡的焦平面上（實際上，光波的光軸是傾斜的）的一個點光源發出球面波的光，透鏡可以被描述為兩個單獨的透鏡組成的，作為如圖4中所示，一個紅色的單色（單一顏色）的點源。 每個透鏡具有不同的焦距（F（A）為最接近的點源在圖4 和f（b）為第二透鏡的鏡頭），和球面波，從第二透鏡（透鏡（b）段）是在焦點為中心，從光軸的透鏡系統也被除去。 作為一個結果，圖4中的S點（1）為中心的球面波由第一透鏡被轉換成平面波是相對于鏡頭的光軸傾斜相同的角度為點源。 第二透鏡轉換成另一種具有點S（2），這也是傾斜相同的角度為點光源為中心的曲率半徑的球面波逐漸從第一透鏡的平面波。 總之，簡單的透鏡（這是圖4中所描述的兩個假設組件鏡片的總和）集中到S點的點源S（1）（2）和反之亦然。 在光學方面，點S（1）S（2）被稱為共軛點 ，并了解發生的事件在顯微鏡的光學列車具有根本的重要性。

要進一步延長共軛點的想法，如果被認為是屬于一組點在一個平面上的垂直于透鏡的光軸的點S（1），則此鏡片會集中到每一個點在一個平面內的點的集合S（2）類似的共軛點。 因此，通過互惠，透鏡還注重平面S的每一個點（2）到（1）中的對應點的集合S從原來的平面。 被稱為在這些密切相關的焦平面的共軛平面，同時對焦。 在一般情況下，在顯微鏡共軛的平面有兩組：一組包含控制光通過的量的光學系統中，形成圖像，而另一組的孔。

因為傳播光波的波列，可以討論光束可以表示為導向正常的波前射線痕跡。 圖4中討論的雙透鏡系統，以考慮到這一事實，可以減少射線的痕跡，如在圖2中所呈現的示意圖中，為了應用的規則的幾何結構，以確定圖像的大小和位置由透鏡形成。 如上所述，兩個有代表性的光線，一個近軸（平行）的光軸和一個穿過透鏡中心的，是必要的，以確定這些參數。

的距離a和b在圖2（F（A）和f（b）在圖4）和透鏡的后焦距（f）的相互關系由簡單的等式適用于所有薄透鏡：

從這個等式中，顯而易見的是，如果后焦距的鏡頭和對象之間的距離是已知的，則透鏡的焦平面之間的距離可以被計算。 此外，由透鏡產生的圖像中的對象的高度除以高度確定的鏡頭的橫向放大率（M）：

當然，剛才所描述的方程的基礎上的假設，即在透鏡系統所包圍兩側的空氣，但是這往往是在光學顯微鏡的情況下，當不使用油，水，或甘油浸泡物鏡。 然而，大多數從低到中等倍率物鏡的共同的顯微鏡不使用除空氣以外的成像介質。 其中，可以是來自于剛剛討論過的簡單的透鏡數學，得出的結論是（或減小尺寸）的圖像的倍率等于透鏡系統的焦距，物體面和焦平面之間的距離除以上的鏡頭的前側（物體側）。 此外，圖像的放大率（或縮小）除以透鏡的焦距的鏡頭，在右側的圖像平面和焦平面之間的距離相等。 這些方程通常用于由具有一個固定的焦距的透鏡系統的放大或縮小圖像尺寸的計算的。 它們也可用于確定從當試樣被放置在對象空間中的一個固定的距離的鏡頭的右側（圖象空間）側的主平面的距離的圖像。

另一個因素是重要的是在顯微鏡的縱向或軸向放大率，被定義為到其相應的試樣中的共軛點的鏡頭沿著軸線的兩個圖像點之間的距離的比例。 在一般情況下，縱向倍率的大小確定的橫向放大率的圖像平面內的小的距離的平方。

結論

單透鏡形成的圖像的能力（如雙凸透鏡）是有用的工具，進行簡單的放大倍率的應用，如放大鏡，鏡片，單鏡頭相機，放大鏡，取景器，和隱形眼鏡。 最簡單的雙重峰（雙透鏡系統）被稱為achromatics的 ，由膠合在一起的兩個透鏡元件，以對軸的外球面像差和色像差校正。 消色差膠合透鏡通常由耦合到一個正的或負的彎月形透鏡或一個平凸透鏡的雙凸透鏡。 三聯消色差透鏡（含三個鏡片）被用作高功率放大鏡和中繼透鏡。更高度校正像差比雙峰，三峰鏡頭組合通常是通過計算機設計技術進行了優化，從根本上消除失真。 更復雜的設備往往采用許多透鏡元件的組合，以提高放大倍數和利用其他的光學性能的圖像。 這些措施包括顯微鏡，望遠鏡，潛望鏡，照相機，望遠鏡，這是使用復合光學系統的許多設備中。

除了上述常見的幾何形狀，鏡片也都可以有各種各樣的其它形狀和尺寸（參見圖5）。 球面球透鏡從所有的入射角表現出相同的性能，有僅依賴于的直徑和折射率的焦距。 通過操作這兩個變量，得到了廣泛的焦距可以與球透鏡，但它們的主要應用是提高利用在電信行業的纖維，發射器和檢測器之間的信號耦合。 半場球透鏡，這是半球形的，在光纖通信的光學，內視鏡，顯微鏡，激光測量系統是有用的。 鼓透鏡產生軸向研磨技術，消除了顯著的部分的透鏡半徑的球透鏡。 這些修改后的透鏡更容易比他們的球透鏡的光學系統在安裝和對齊。

柱面透鏡，所生產各種各樣的形狀和尺寸，包括扁平的一個表面上的圓筒，將光線聚焦在一個單一的平面的一部分。 因為這些鏡頭是能夠在單一方向上的放大倍率，可以利用拉伸圖像。 此外，柱面透鏡的點光源轉換成一條線的圖像，使它們可用作激光線發生器，或將光線聚焦成一個狹縫。 其他透鏡形狀錐 ， 棒 ， 非球面光學元件。 錐鏡片可以360度全方位照明和圖像處理應用。 棒狀透鏡隨著類似柱面透鏡的光學性能，將關注的焦點直徑的光通過準直成一條線。 片非球面鏡片，它可以在一個大的數值孔徑的各種生產，消除球面像差和改進聚焦和準直精度。 這些透鏡往往利用高效率的照明系統中，作為電容元件。

形成圖像的光學元件，顯微鏡光學列車照明器（聚光鏡）的透鏡，聚焦透鏡（物鏡），和目鏡透鏡。 雖然通常被描述為成像元件，這些單獨的透鏡元件和組的成像特性是具有根本的重要性確定顯微鏡所產生的圖像的最終質量。